Summary:
- 语法制导的定义
- 构造语法树
- S-属性定义、L-属性定义
- 自顶向下计算属性
- 自底向上计算属性
语法制导定义
语法制导翻译是一种搭建在语法分析基础上的翻译技术。
思路:给每个符号(特别是非终结符)设置一系列属性 attribute,在语法翻译的时候对属性进行求值。
语法制导定义 SDD 是 CFG 的推广:
- 语法符号 - 属性,定义时需要说明其意义和类型
- 综合 synthesized,由子节点属性计算,命名为 val (value)
- 继承 inherited,由 parent 和 sibling 属性计算,命名为 in (inherited)
- 表达程序结构在上下文中的相互依赖关系
- terminal 只有综合属性,由词法分析器提供;开始符号没有继承属性。
- production - 语义规则,用于计算属性
- 每个 production 关联一个或多个语义规则
- 语义规则的执行反映属性之间的关系
- 依赖图 dependency graph
- 注释语法树 annotated parse tree,节点带有属性值的分析树
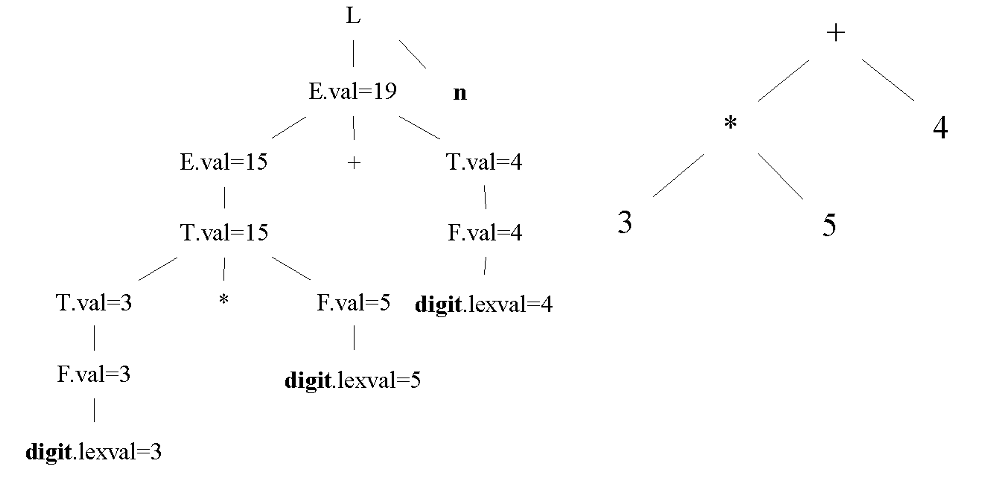
SDD 的格式是一个表,见下面两个例子。
e.g. 要对表达式求值,可以定义语义规则如下:
要定义变量,可以定义语义规则如下:

可见,翻译目标决定了语义规则。
如果一条语义规则的作用和求值无关,如打印一个值或向符号表中添加记录,则成为 production 左侧 non-terminal 的虚拟综合属性,常见的有:
- print (text) 打印 text
- addtype (id.entry, type)
- 在符号表中为符号 id 添加符号类型(变量类型)type
- id. entry 指明符号 id 在符号表中的入口
依赖图
属性 b 依赖属性 c,则 b 应该在 c 之后计算;依赖图是表示这种依赖关系的有向图。
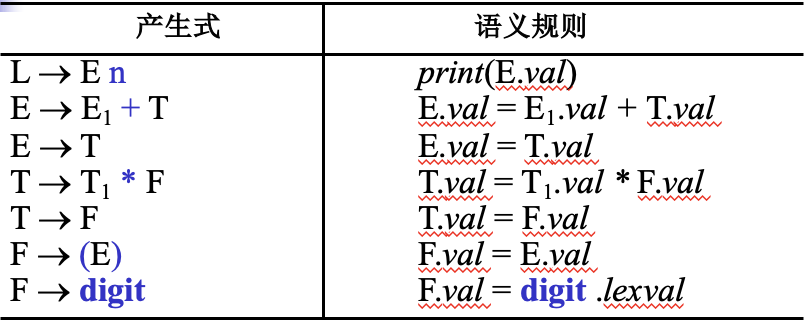
e.g. 变量定义的依赖图
符号左侧为继承属性,右侧为综合属性(包括虚拟综合属性)
如果依赖图无环,则存在一个拓扑排序,即为这些属性值的计算顺序。
语法制导翻译的一般步骤:
- 文法
- 注释语法树
- 依赖图
- 拓扑排序
- 语义规则计算顺序
- 输入串翻译结果
构造语法树
语法树是仅由终结符构成的分析树的压缩形式;
自身可以表示运算的优先级,所以所有括号都可以省略。
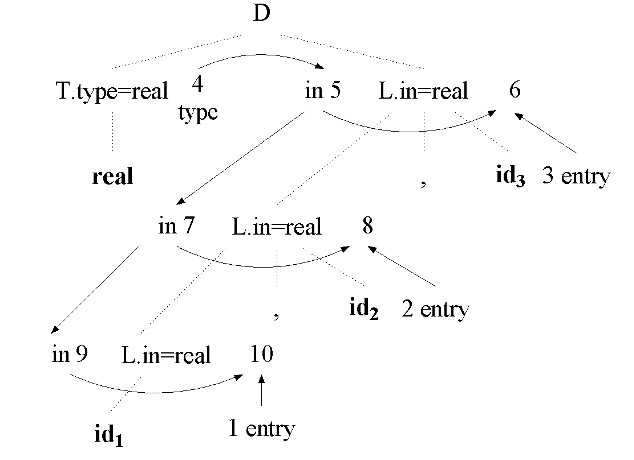
e.g.
用有向无环图 DAG 表示表达式:
- 对语法树提取公共表达式
- 可能出现一个节点有多个 parent 的情况
- 构造节点前检查是否已经构造相同节点
e.g. i = i + 10
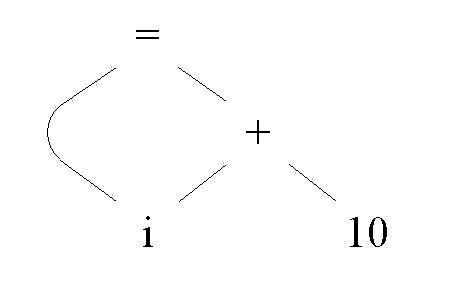
S-属性定义和 L-属性定义
翻译模式
又叫翻译方案,将语义规则嵌入 production 右部适当的位置,指明计算顺序;相当于在 SDD 的基础上添加了执行语义规则的时机。
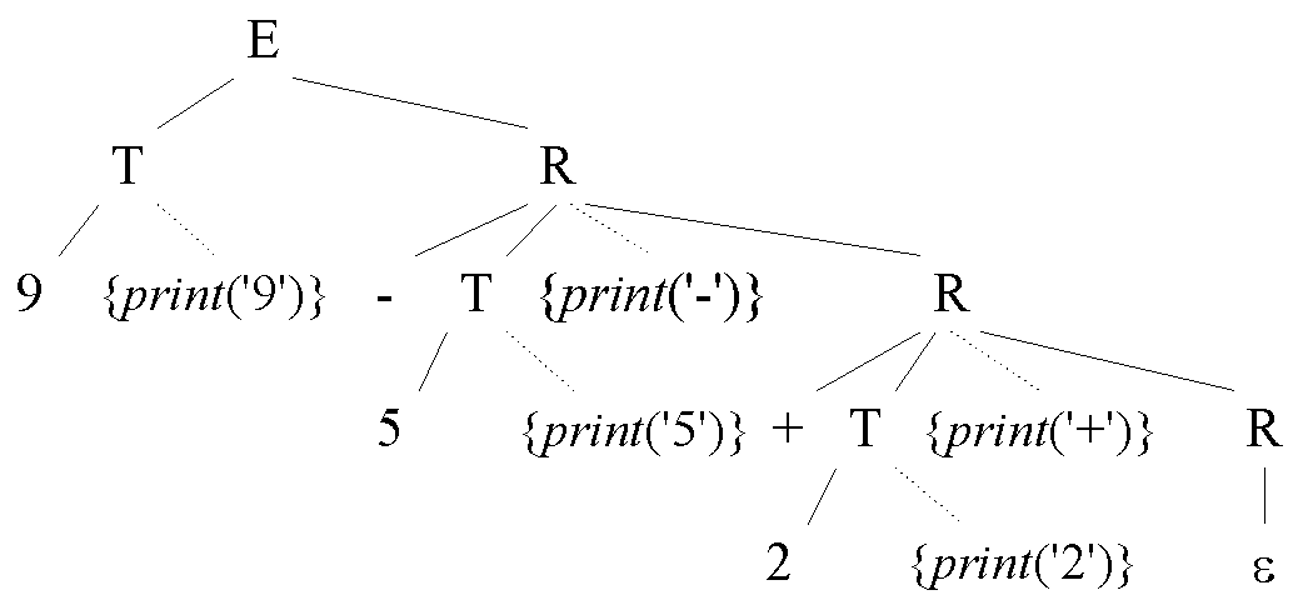
e.g.
E -> T R
R -> op T {print(op.lexeme)} R | e
T -> num {print(num.val)}
翻译模式的语法分析树,为每个语义规则构造节点,使用虚线与 production 头部相连:
S-属性定义
如果一个 SDD 仅使用了综合属性,则称其为 S-属性定义;因为属性自底向上计算,所以通常使用自底向上的方法求值。
S-属性定义可以和 LR 分析器结合:
- 在栈中保存语法符号的属性值
- 规约时,利用栈中语法符号(production 右部)属性值计算新的(左部符号的)综合属性值
- 翻译模式:因为调用一个 production 时,右部所有符号的属性都已经计算完毕,所以 production 对应的语义规则都直接添加到末尾即可。
- 注意仍然需要拓广文法!
定义如下变量:
- val 属性栈
- top 规约前栈顶
- ntop 规约后栈顶
那么可以用形如 val[top-?] 访问栈中内容,如 val[ntop] = val[top-2] + val[top]
e.g. 表达式计算语义规则的代码段

L-属性定义
如果一个 SDD 仅使用了综合属性,或所有继承属性只需要其左边符号的属性,则此 SDD 为 L-属性定义
所有 S-属性定义都是 L-属性定义
L-属性定义的属性计算顺序:DFS 遍历分析树,这样如果所有继承属性都只用到左 sibling 的属性,则继承属性可计算:
procedure dfsvisit(n:node)
{
for n 的每个孩子,由左至右 do
{
计算 m 的继承属性;(利用 n 的继承属性和 m 的左sibling的属性)
dfsvisit(m);
}
计算 n 的综合属性;
}
翻译模式:
- production 右部符号的继承属性必须在这个符号以前的语义规则中被算出来
- 语义规则不能(直接或间接地)引用它右边的符号的属性
- 左部 non-terminal 的综合属性,必须在其依赖的所有属性计算完毕后才能计算,一般放在右部末尾
自顶向下计算属性
基于递归下降的预测分析
要求消除左递归
-> 一般性方法:已知翻译模式
A -> A1Y {A.a = g(A1.a, Y.y)}
A -> X {A.a = f(X.x)}
消除左递归:
A -> XR
R -> YR1
R -> e
把 A1 消除,增加了 R -> 如何通过 R 传递 A1 的属性?
为 R 设置:
- 继承属性 R.i 保存中间结果
- 综合属性 R.s 向上传递最终结果
把中间结果保存在 R.i 中一路向下计算,算出最终结果后,传递给 R.s,然后再一路向上传回根节点。
翻译模式:
A -> X {R.i = f(X.x)} R {A.a = R.s}
R -> Y {R1.i = g(R.i, Y.y)} R1 {R.s = R1.s}
R -> e {R.s = R.i}
e.g.
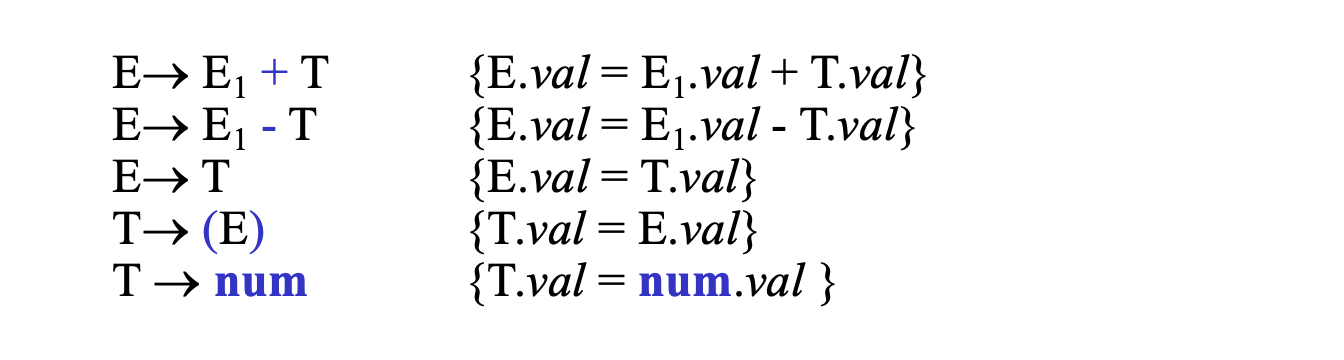
消除左递归后:
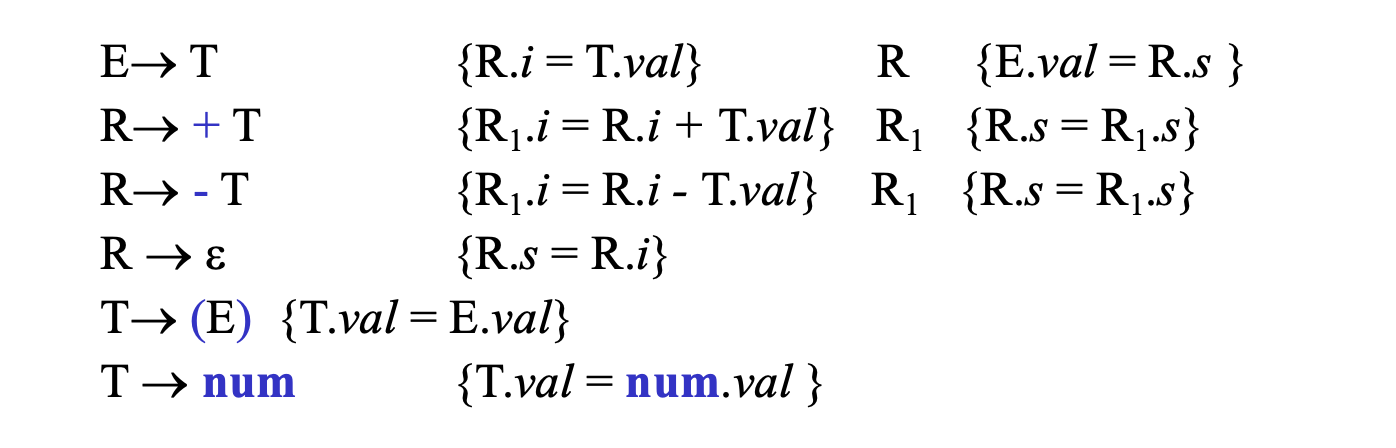
语法树:
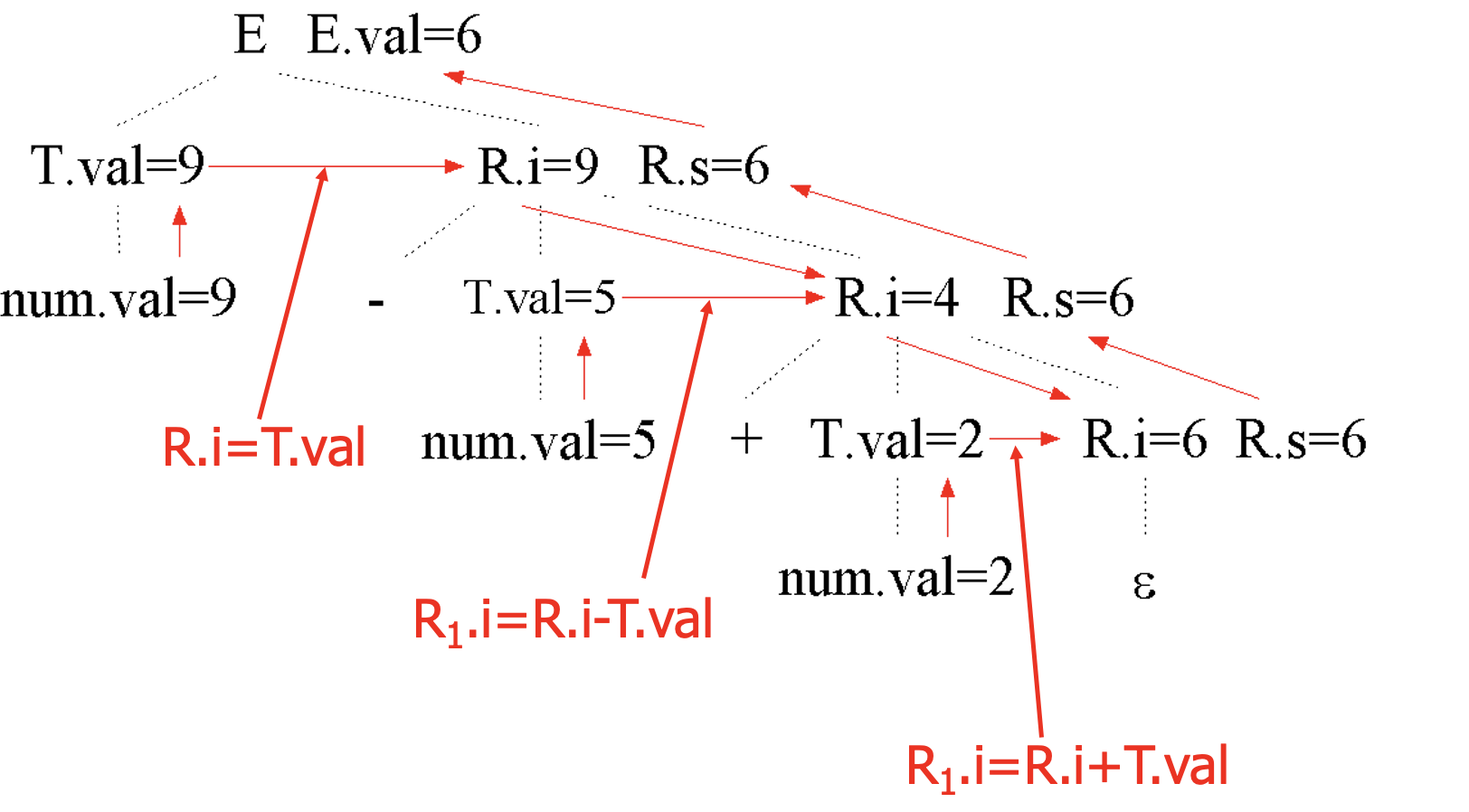
翻译模式:为每个 non-terminal 建立一个函数
- 参数为此 non-terminal 的继承属性
- 返回值为综合属性
- production 中语法符号的属性 —— 函数局部变量
- 函数体结构和递归调用预测分析类似,根据当前输入符号确定使用哪个 production
自底向上计算属性
思路:移走翻译模式中嵌入的语义规则,改写 SDD 为 S 属性定义
没有继承属性的情况
e.g. 已知如下 L-属性定义:
E -> TR
R -> + T {print('+')} R | - T {print('-')} R | e
T -> num {print(num.val)}
语义规则阻碍了此文法成为 S-属性定义
(在移入栈过程中根本不知道将来会形成哪个 production,无法执行嵌入的语义规则)
-> 加入空 production,取走语义规则
E -> T R
R -> + T M R | - T N R | e
T -> num { print(num.val)}
M -> e { print(‘+’) }
N -> e { print(‘-’) }
属性值的计算只在规约时进行
有继承属性的情况
用 C->XYZ 规约时如果需要 C 的继承属性,但 C 不在栈中,就需要寻找 C 在右部的 production(C 的继承属性依赖于其 parent 和左 sibling),但 parent 也不在栈中,进入一个循环
-> 复写规则
e.g.1. 继承属性位置可确定的情况

由于 L.in = T.type,而且 T 是 L 的左 sibling,在对关于 L 的 production 规约、需要 L 的继承属性 in 时,T 一定已经在栈中,可以用 T.type 代替 L.in:

e.g.2. 继承属性位置不可确定的情况
S -> aAC {C.i = A.s}
S -> bABC {C.i = A.s}
C -> c {C.s = g(C.i)}
不确定 B 是否在栈中,就无法确定 A.s 在 top-1/top-2
-> 新建符号 M 作为跳板:
S -> aAC {C.i = A.s}
S -> bABMC {M.i = A.s; C.i = M.s;}
C -> c {C.s = g(C.i)}
M -> e {M.s = M.i}
M 作为桥梁衔接 A 和 C,M 访问 top-2 来访问 A.s,这样 C 只要访问 top-1 就必然能够访问到 A.s。
e.g.3. 继承属性使用函数赋值(非复写规则)
S -> aAC {C.i = f(A.s)}
属性栈里只保存了 A.s,没有保存 C.i
-> 新建符号 N 作为跳板:
S -> aANC {N.i = A.s; C.i = N.s}
N -> e {N.s = f(N.i)}
添加一个符号保存运算结果为 N.s,这样 C.i 就可以通过 top-1 访问。