编译原理笔记04：语法分析

Summary：

上下文无关文法
语法分析
- 自顶向下
- 自底向上：LR (0) / SLR / LR (1) / LALR
语法错误处理

上下文无关文法

正则表达式的能力不足 -> ch2 CFG

凡是正则表达式能表示的语言，都能用 CFG 表示：可以机械地由 NFA 变换而得，NFA 字母表视为 terminal 集合

推导：最左推导（每次替换最左边的 non-terminal）、最右推导（规范推导）
写出分析树 parse tree
二义性：不止一种最左/右推导

句型 sentential form、句子 sentence、语言

消除二义性 eliminating ambiguity

不存在一个算法，能在有限步骤内确切地判定任给的一个 CFG 是否为二义性文法；二义性的消除也没有规律可循，但是可以总结出一些较为通用的手段。

改写为非二义文法

划分优先级和结合性
- 引入一个新的 non-terminal，增加一个子结构并提高一级优先级（优先级的判断）；
- 递归 non-terminal 在 terminal 左边，运算具有左结合性，否则具有右结合性。

e.g. E → E+E|E*E|(E)|-E|id

优先级从低到高：[+], [*], [(),-, id]
结合性：左结合 [+,*]，右结合[-]，无结合[id]
non-terminal 与运算：
- E:+ E production 左递归
- T:* T production 左递归
- F:(),-,id F production 右递归

E -> E+T | T
T -> E*F | F
F -> (F) | -F | id

e.g. dangling else 问题：then 的个数多于 else，后者不知道和哪个 then 结合
就近匹配，规定 else 和最近的 then 匹配（右结合）

缺点：引入更多 non-terminal 使得 parse tree 更深、更难理解

为文法符号规定优先级和结合性 yacc 采用的就是这种方式：

%left '+''*'
%right '-'

修改语言的语法（表现形式被改变）

明确给出结束标志
给表达式加括号

语言和文法

词法分析和语法分析的分离

正规语法是 CFG 的特例
用正则表达式定义词法的若干好处（简单、简洁、高效）
软件工程上的好处（模块、可移植）

CFG 的表达能力还是不足 -> 非上下文无关文法

语法分析

自顶向下

预处理：消除左递归、提取左因子

左递归 left recursion：存在 non-terminal $A$ s.t. $A\rightarrow^{+}A\alpha$，其中 $\alpha$ 是文法符号串
top-down 分析无法处理左递归，会陷入无限循环
左递归分为两种：直接、间接

直接左递归 immediate left recursion
文法中存在 $A\rightarrow A\alpha|\beta$，其中文法符号串 $\beta$ 不以 $A$ 开头
消除：写成 $A\rightarrow \beta A’, A’\rightarrow\alpha A’|\epsilon$
间接左递归
形如 $S\rightarrow Aa|b, A\rightarrow Sd|\epsilon$
先变换成直接左递归 $S\rightarrow Aa|b, A\rightarrow Aad|bd|\epsilon$
再消除左递归 $S\rightarrow Aa|b, A\rightarrow bdA’|A’, A’\rightarrow adA’|\epsilon$

提取左因子 left factoring：$A\rightarrow\alpha\beta_{1}|\alpha\beta_{2}$，不知道用哪个来替换
提取最长公共前缀 $A\rightarrow\alpha A’, A’\rightarrow\beta_{1}|\beta_{2}$
e.g. hanging else

LL (1) 文法和递归下降的预测分析

L-left to right; L-leftmost derivation
LL (1) 文法的性质：不是二义的、没有左公共因子、不含左递归

通过向前看一个符号确定 production，消除回溯。
e.g. 当前句型是 xAb，输入是 xa…，那么要选择 production $A\rightarrow\alpha$ 的必要条件是：

$\alpha\rightarrow a\dots$
$\alpha\rightarrow\epsilon$，且 $\beta$ 以 a 开头，即在某个句型中 a 跟在 A 之后

定义函数：

$FIRST(\alpha)$

定义：$\alpha$ 推出的非空串中首 terminal、以及 $\alpha$ 推出空串时的 $\epsilon$ 组成的集合（只能包含终结符和 $\epsilon$）
- 形式化定义： $FIRST(\alpha)=\{\alpha|\alpha\rightarrow*\alpha\dots,\alpha\in V_{T}\}\cup\{\epsilon|\alpha\rightarrow*\epsilon\}$
意义：下一个输入符号 a，若 $a\in FIRST(\alpha)$，选择 production $A\rightarrow\alpha$
计算方法：
- X 是 terminal，$FIRST(X)={X}$
- X 是 non-terminal，且 $X\rightarrow Y_{1}Y_{2}\dots Y_{k}$
  - 如果 $\alpha\in FIRST(Y_{i})$ ，且 $\epsilon$ 在 $FIRST (Y_{1}),\dots,FIRST(Y_{i-1})$ 中，则加入 $\alpha$
  - 如果 $\epsilon$ 在 $FIRST (Y_{1}),\dots,FIRST(Y_{k})$ 中，则加入 $\epsilon$
- X 是 non-terminal，且 $X\rightarrow\epsilon$，则加入 $\epsilon$

$FOLLOW(A)$

定义：可能在某些句型中紧跟在 A 右边的终结符的集合
- 形式化定义：$FOLLOW(A)=\{\alpha|S\rightarrow*\dots A\alpha\dots,\alpha\in V_{T}\}\cup\{S\rightarrow*\dots A\}$
意义：下一个输入符号 b， $A\rightarrow\alpha$ 且 $\alpha\rightarrow\epsilon$ 时，若 $b\in FOLLOW(A)$，可以选择 $A\rightarrow\alpha$
计算方法：
- 将右端结束标记 $ 加入 $FOLLOW(S)$
- 按下述两个规则迭代，直到所有的 $FOLLOW$ 集合都不再增长：
  - 若 $A\rightarrow\alpha B\beta$，则将 $FIRST(\beta)$ 中所有非 $\epsilon$ 的 terminal 加入 $FOLLOW(B)$
  - 若 $A\rightarrow\alpha B$ 或（$A\rightarrow\alpha B\beta$ 且 $\epsilon\in FIRST(\beta)$），则将 $FOLLOW(A)$ 中所有符号都加入 $FOLLOW(B)$

LL (1) 文法的定义：任何两个 production $A\rightarrow\alpha|\beta$ 都满足下列条件：

$FIRST (\alpha)\cap FIRST (\beta)=\emptyset$
若 $\beta\rightarrow*\epsilon$ ，则 $FIRST (\alpha)\cap FOLLOW (A)=\emptyset$；反之亦然

非递归的预测分析表

列是 non-terminal，行是 terminal 或结束标记 $，每个格子 $M[A,a]$ 是 non-terminal->terminal 的 production $A\rightarrow\alpha$（即当前输入是 a 时，采用该 production）

对每个 production $A\rightarrow\alpha$：

对 $FIRST(\alpha)$ 中的每个 terminal a，将 $A\rightarrow\alpha$ 加入 $M[A,a]$ 中
如果 $\epsilon$ 在 $FIRST(\alpha)$，则对于 $FOLLOW(A)$ 中的每个符号 b，将 $A\rightarrow\alpha$ 也加入 $M[A,b]$ 中
其他没有定义的条目都是 error

采用一个符号栈保存分析时的处理过程：

初始化，栈中仅包含开始符号 S
如果 top 元素是 terminal，和输入匹配
如果 top 是 non-terminal，使用预测分析表选择 production，在栈顶用右部替换左部，将右部按倒序 push 入栈

分析表驱动的预测分析器的模型如：

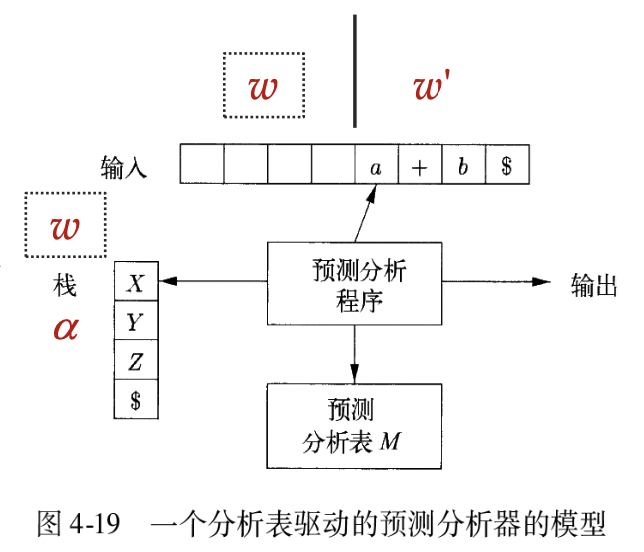
e.g. 输入：id+id*id

什么时候报错？

栈顶的 terminal 和下一个输入符号不匹配；
栈顶是 non-terminal A，输入符号 a，而 $M[A,a]$ 为空。

错误恢复：采用 panic mode，抛弃输入记号，直到其属于某个指定的同步记号 synchronizing tokens 集合为止。

总而言之，自顶向下语法分析的步骤大概如：

消除文法的二义性
消除左递归，提取左公共因子
计算 FIRST 集和 FOLLOW 集
进行分析（递归下降/预测分析表）

自底向上

bottom-up 的移入-规约 shift-reduce 分析：从串 w 开始规约到开始符号 S
reduction 步骤：一个与 production 右部匹配的子串替换为左部符号
是最右推导的逆过程，比 top-down 方法更一般化

问题：什么时候规约（规约哪些字符串）？规约到哪个 non-terminal？

把输入从左到右扫描，反向构造出一个最右推导。
句柄 handle：最右句型中和某个 production 匹配的子串，对它的规约代表了该最右句型的最右推导的最后一步。
即：若 $S\rightarrow\alpha A\omega\rightarrow\alpha\beta\omega$，那么紧跟在 $\alpha$ 之后的 $\beta$ 是 $A\rightarrow\beta$ 的一个 handle
在最右句型中，handle 右边仅含 terminal（尚未处理的输入串）
e.g.输入 id*id

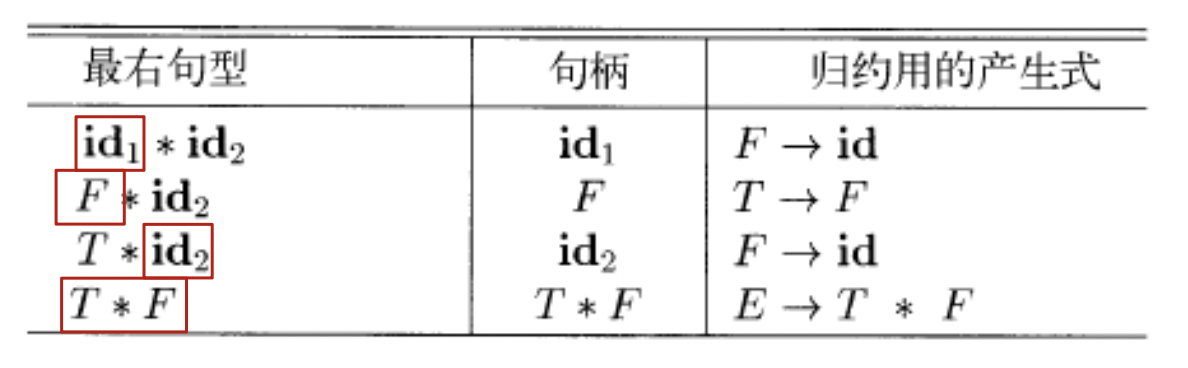
移入-规约

也采用一个栈保存规约/扫描移入的符号：

栈中符号从底向上和待扫描的符号组成一个最右句型
开始：栈中只包含 $，输入为 $\omega\$$
结束：栈中为 S$，输入为 $
分析过程中不断移入符号，并在识别到 handle 时进行规约
- handle 被识别时总在栈顶

分析动作：

移入 shift：将下一个输入符号移入栈顶
规约 reduce：弹出 handle，规约为相应的 non-terminal，入栈
接受 accept：分析成功完成
报错 error

e.g.

移入-规约冲突：即使知道了栈中所有内容，以及接下来 k 个输入符号，仍然不知道是该移入还是规约/该按照哪个 production 规约
栈顶形成不同的 handle，或 handle 是不止一个 production 的右部

如何快速识别栈顶是否形成 handle？引入状态。

LR 语法分析

LR (k)：L-left to right; R-rightmost derivation in reverse; k 最多向前看 k 个符号
只考虑 k<=1 的情况
最通用的无回溯移入-规约分析技术

基本思想： 用状态刻画栈中内容，每个状态都对应一个文法符号（初始状态 $s_{0}$ 除外），根据栈顶状态判断是否形成 handle
将符号写作状态的意义是？
通过类似于有限状态机的输入-动作（移入/规约）机制，进行语法分析。

构建 LR 语法分析表，两个部分：

动作 ACTION：两个参数状态 $s_{m}$ 和 terminal $a_{i}$，$ACTION[s_{m},a_{i}]$ 表示在该状态下面对输入符号 $a_{i}$ 应该采取的动作。
- 移入 $s$：执行移入动作，将输入 $a_{i}$ 对应的状态 $s$ 入栈
- 规约 $A\rightarrow\beta$：将栈顶的 $\beta$ 规约为 A，弹出 $r=\mid\beta\mid$ 个状态，压入状态 $s=GOTO[s_{m-r},A]$
- 接受、报错
转向 GOTO：两个参数状态 $s_{m}$ 和 non-terminal A，$GOTO[s_{m},A]$ 表示在该状态下当前栈顶 handle 规约为 A 后应该转向哪个状态。

LR 语法分析器的结构 configuration 包括栈中内容 $s_{0}s_{1}\dots s_{m}$ 和余下输入 $a_{i}a_{i+1}\dots a_{n}\$$，语法分析器查询条目 $ACTION[s_{m},a_{i}]$ （栈顶状态，第一个输入符号）确定下一步动作。

e.g.

注：表中 $s_{i}$ 表示移入，$r_{j}$ 表示按第 j 号 production 规约，acc 表示接受。

对处理过程的说明：

移入如 4-5 步，栈内状态[0 2]，符号 T，输入 *id+id$，那么：

查询 $ACTION[2,*]=s_{7}$
压入状态 7

规约如 2-3 步，栈内状态[0 5]，符号 id，输入 *id+id$，那么：

查询 $ACTION[5,*]=r_{6}$ 规约
按 $r_{6}$ 执行规约 $F\rightarrow id$：
- 将 id 规约为 F
- 弹出 1 个状态 5
- 查询 $GOTO[0,F]=3$
- 压入状态 3

如何构造 LR 分析表？

LR (0) 和 SLR

活前缀 viable prefix：不超过最右 handle 右端的前缀

viable: something that is viable is capable of doing what it is intended to do.

形式化定义：规范句型 $\gamma\beta\omega$，$\beta$ 为 handle，$\gamma\beta$ 的任何前缀（包括 $\epsilon$ 和其自身）都是活前缀，$\omega$ 仅包含 terminal，即输入缓冲区中剩下的符号串
在 LR 语法分析中，活前缀就是从栈底到栈顶的所有文法符号连接形成的串。

LR 分析表的转移函数 GOTO 本质上是识别活前缀的 DFA。
在 LR (1) 方法中，要看到 production 右部推出的整个 terminal 串，才会确定用这个 production 规约。

LR (0) 项目：在右部的某个地方加点（表示分析所处位置）的 production
e.g. $[A\rightarrow\alpha·\beta]$ 表示已经扫描/规约到了 $\alpha$，并期望在接下来的输入中经过扫描/规约得到 $\beta$，然后把 $\alpha\beta$ 规约到 A。
或：·之前已形成活前缀，在栈中；之后尚未分析，对应的 terminal 串在输入缓冲区

文法天然有一个识别活前缀的 NFA：
e.g. 文法 $S\rightarrow aABe; A\rightarrow Abc|b; B\rightarrow b$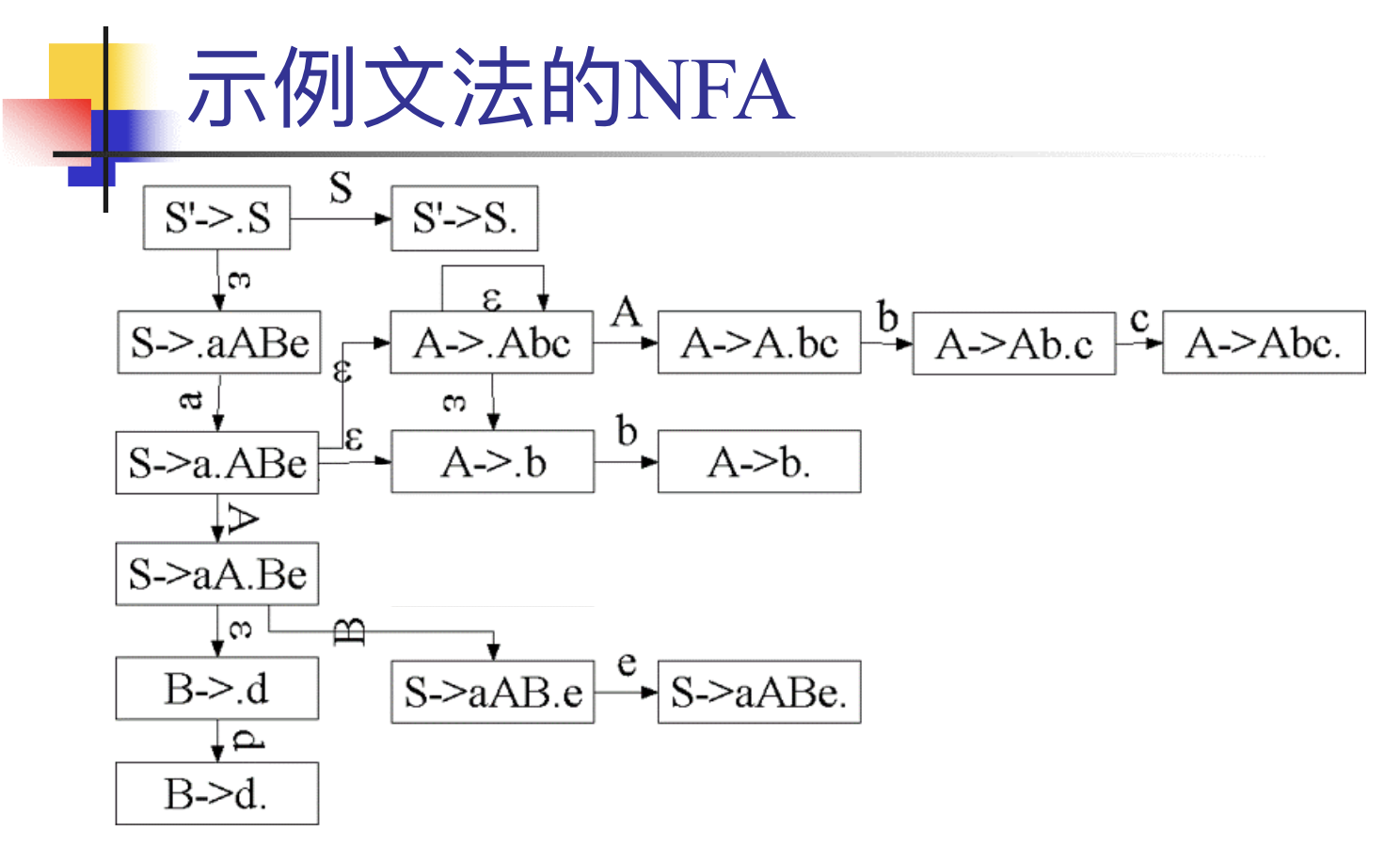

DFA 的状态集：LR (0) 项集规范族 canonical LR (0) collection
核心计算：项集闭包 closure 和 goto 函数
本质上是一个子集构造法过程，上述的 NFA->DFA

增广文法 augmented grammar：G 的增广文法 G’是在 G 中增加新开始符号 S’，并加入 production $S’->S$ 得到的。
项集闭包 closure：若 I 是文法 G 的一个项集，closure (I) 就是根据以下算法从 I 构造得到的项集：

意义：$A\rightarrow\alpha·B\beta$，希望看到由 $B\beta$ 推导出的串，那首先要看到 B 推导出的串，因此要加上 B 的各个 production 对应的项。
production 对应的状态转换没有 push 任何符号，$\epsilon$ 边
goto 函数：I 是一个项集，X 是一个文法符号，则 $GOTO (I, X)$ 定义为 I 中所有形如 $[A\rightarrow\alpha·X\beta]$ 的项所对应的项 $[A\rightarrow\alpha X·\beta]$ 的集合的闭包。

求 LR (0) 项集规范族的算法：从初始项集开始，不断计算各种可能的后继，直到生成所有的项集。

项集规范族构造示例：

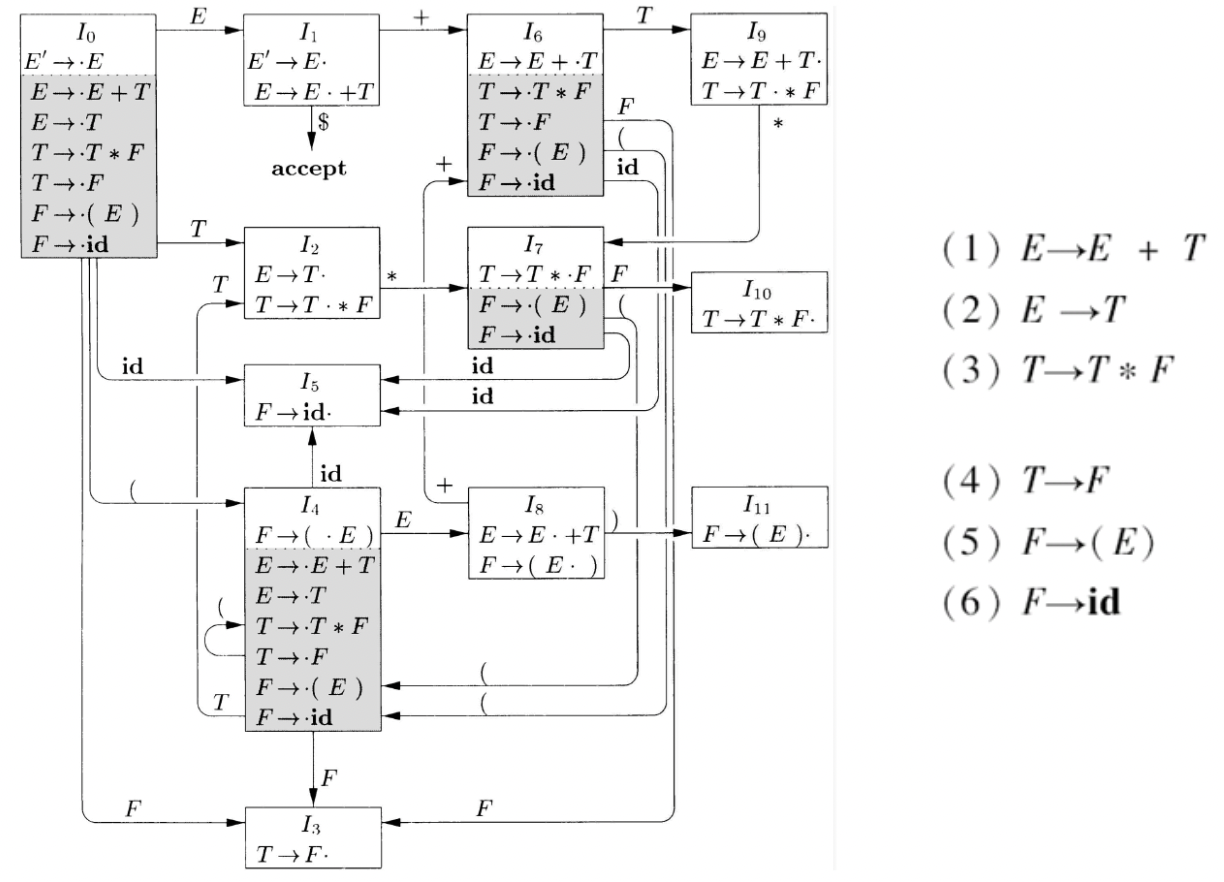
基于 LR (0) 项集规范族，可以构造 LR (0) 自动机：

每个项集对应于自动机的一个状态
如果 $GOTO (I, X)=J$，那么从 I 到 J 有一个标号为 X 的转换
开始状态为 $[S’\rightarrow ·S]$ 所在的项集

LR (O) 不向前看：如果某个状态存在规约项目，那么此状态在 action 表中所有条目都是该规约动作。
问题：容易产生冲突，e.g. 某个状态 i 包含 $[A\rightarrow\alpha·]$ 和 $[A\rightarrow·c]$，那么 $ACTION[i,c]$ 既应该移进 c，又应该规约 A。

为了解决冲突，基于 LR (0) 自动机，进一步构造 SLR 语法分析表：

构造增广文法 G’的 LR (0) 项集规范族 $\{I_{0},I_{1},\dots,I_{n}\}$
状态 i 对应项集 $I_{i}$，相关的 action/goto 表条目如：
- $[A\rightarrow\alpha·a\beta]$ 在 $I_{i}$ 中，且 $GOTO(I_{i},a)=I_{j}$，则 $ACTION[i,a]$ =‘移入 j’
- $[A\rightarrow\alpha·]$ 在 $I_{i}$ 中，那么对 $FOLLOW(A)$ 中所有 a，$ACTION[i,a]$ =‘按 $A\rightarrow\alpha$ 规约’
- 如果 $[S’\rightarrow S·]$ 在 $I_{i}$ 中，那么 $ACTION[i,$]$ =‘接受’
- 如果 $GOTO(I_{i},A)=I_{j}$，那么在 GOTO 表中，$GOTO[i,A]=j$
空白条目设为 error

如果 SLR 分析表没有冲突，该文法就是 SLR 的；
SLR 文法一定是非二义性的，但是反之不一定。

SLR 解决冲突的思想：如果要把 $\alpha$ 规约成 A，那么后面必须是 $FOLLOW(A)$ 中的 terminal，否则只能移入。
也就是说，判断是规约还是移进时，SLR 试图通过向前看一位确定操作。

但是，仍然可能存在无法通过向前看一位解决的冲突：
状态中包含 $[A\rightarrow\alpha·]$ 时，下一个符号 a 必须在 $FOLLOW(A)$ 中，才能按照 $A\rightarrow\alpha$ 规约。

但如果此时对 a 还有其他移入/规约操作，就会出现冲突；
如果此时栈中符号串是 $\beta\alpha$，如果 $\beta Aa$ 不是任何最右句型的前缀，那么即使 a 在 $FOLLOW(A)$ 中，也不应该按 $A\rightarrow\alpha$ 规约。

答题流程：

拓广文法（切记勿忘）
对任意已知文法，假设它的起始符号为 S，则添加一个生成式 $S’\rightarrow S$ 用来产生接受项目
把文法转换成每个 production 只有一个候选式的形式，标号，以便分析表引用
构造 LR (0)项集规范族及其 DFA
切记不存在 SLR (1)项目集规范族
判断 LR (0) 项集规范族中有没有冲突（即，不向前看就没法解决的冲突），如果有，写出冲突类型；没有冲突就能构造 LR (0) 分析表
如果存在冲突，冲突是否能通过向前看一位解决。如果能，就可以构造 SLR (1)分析表；如果不能，尝试使用后文的 LR (1)分析法。

LR (1) 和 LALR (1)

LR (1) 分析法：始终向前看一个符号
解决冲突的能力是最强的，但是状态会非常多

LR (1) 项包含了更多信息，添加某个项时把期望的向前看符号也加入项中，相当于分裂一些 LR (0) 状态，精确指明应该在何时规约。
$[A\rightarrow\alpha·\beta, a]$ 表示如果将来要按照 $A\rightarrow\alpha\beta$ 进行规约，规约的下一个输入符号必须是 a（可以是 terminal 或者 $）；$\beta$ 非空时，移入动作不考虑 a，a 传递到下一状态。
特别地，包含拓广符号 S’的状态为：$[S’\rightarrow ·S,\$]$

LR (1) 项集族的构造和 LR (0) 类似，但 closure 和 goto 的计算有所区别：

LR (1) 项集的 closure 算法：

意义：要看到 B 推导出的串，就需要加入 B 的所有 production；B 后面跟着的是 $\beta\alpha$，那么下一个输入符号必须在 $FIRST(\beta\alpha)$ 中。
LR (1) 项集的 goto 算法：和 LR (0) 基本相同

LR (1)项集规范族的构造算法和 LR (0)相同，不再赘述；初始状态是 $[S’\rightarrow·S,\$]$ 所在的项集。

基于 LR (1) 项集规范族，可以构造 LR (1) 语法分析表，流程和 LR (0) 比较接近，主要区别在规约动作的判断：

构造增广文法 G’的 LR (1) 项集规范族 ${I_{0},I_{1},\dots,I_{n}}$
状态 i 对应项集 $I_{i}$，相关的 action/goto 表条目如：
- $[A\rightarrow\alpha·a\beta,b]$ 在 $I_{i}$ 中，且 $GOTO(I_{i},a)=I_{j}$，则 $ACTION[i,a]$ =‘移入 j’
- $[A\rightarrow\alpha·,a]$ 在 $I_{i}$ 中，那么 $ACTION[i,a]$ =‘按 $A\rightarrow\alpha$ 规约’
- 如果 $[S’\rightarrow S·,\$]$ 在 $I_{i}$ 中，那么 $ACTION[i,\$]$ =‘接受’
- 如果 $GOTO(I_{i},A)=I_{j}$，那么在 GOTO 表中，$GOTO[i,A]=j$
空白条目设为 error

LR (1) 的不便之处是状态要远多于 LR (0)；LALR 的意思是 lookahead-LR，是一种介于 LR (1) 和 SLR 之间的的方法，合并了 LR (1)中的某些状态来简化程序；
它的分析表和 SLR 一样大，但分析能力更强，已经可以处理大部分程序设计语言。

LALR 简化项集的思想是：寻找具有相同核心（core，即项的第一个分量，或 LR (0) 项集）的 LR (1) 项集，并将它们合并为同一个项集，使得分析表既保持了 LR (1) 项中的向前看符号信息，又将状态数减少到和 SLR 一样多。

e.g. 存在如下项集规范族：
$$I_{4}={[C\rightarrow d·,c]\ [C\rightarrow d·,d]}$$
$$I_{7}={[C\rightarrow d·,\$]}$$
即，状态 4 和 7 有相同的核心 $C\rightarrow d·$，区别在于状态 4 在下一个输入符号是 c 或 d 时规约，$ 时报错，状态 7 则正相反；于是，可以将它们合并为一个项集：

$$I_{47}={[C\rightarrow d·,c]\ [C\rightarrow d·,d]\ [C\rightarrow d·,\$]}$$

被合并项集的 goto 目标也随之合并。
-> 可能出现的问题是会引发规约-规约冲突，即不能确定按照哪个 production 规约：

实际分析中，处理语法正确的输入时，LALR 和 LR (1) 的动作序列完全相同；处理错误输入时，LALR 可能会在合并同心集时做了不必要的规约，导致延迟发现错误。

语法错误处理

预测分析中的错误恢复：不仅要报错，而且能进行恢复处理后继续语法分析过程
错误恢复时可用的信息：栈中符号、待分析的符号
两类方法：panic mode，短语层次的恢复

panic mode

思路：如果已经不可能在输入前缀中找到和某个 non-terminal 对应的串，就将其跳过，假装已经找到了它，然后继续分析
指定的同步词法单元 synchronizing token 就是这个跳过的程序结构的结束标志。
-> 确定文法符号 A 的同步词法单元：

$FOLLOW(A)$ 中的所有符号
$FIRST(A)$ 中的所有符号（遇到时可能表明前面的符号是多余的）
高层次的 non-terminal 的开始符号加入低层次 non-terminal 的同步集合
- e.g. 语句开始符号，if/while, etc.
对 terminal：栈顶的 terminal 匹配错误时可以直接弹出这个符号，并且假装已经插入了它

假定同步集合就是 $FOLLOW$ 集，那么恢复策略如：

假设栈中符号 $\alpha$，输入符号 a，但 $\alpha a$ 不是任何最右句型的前缀；
从栈顶往下扫描，找到状态 s，存在对应某个 non-terminal A 的 goto 函数
丢弃输入符号直到找到一个 $b\in FOLLOW(A)$，将 $GOTO[s,A]$ 压栈，继续分析

即，假装正试图规约到 A 但遇到语法错误，丢弃已分析的栈和未分析的输入，假装找到了 A 的实例。

短语层次的恢复

在预测语法分析表的空白条目中插入错误处理函数的指针，后者可以改变、插入或删除输入中的符号，并发出错误消息。
恢复策略：检查每个空白条目，根据语言特性确定程序员最可能犯了什么错误，然后构造适当的恢复程序。