Summary:
- token 及属性
- 正则表达式与转换图
- Lex 程序
- 有限自动机
- 正则表达式到 NFA
- NFA 到 DFA
- DFA 的化简
token 及属性
- 词法记号/单词 token:字符串集的分类
- <identifier>,<number>
- <记号名[, 属性值]>
- 模式 pattern:描述字符串集如何分类为 token 的规则
- 正则表达式,[A-Z]*
- 词法单元/词素 lexeme:程序中实际出现的字符串,匹配 pattern 分类为 token
- i, count, name, 60…
- 保存进符号表;返回给语法分析器
- 词素的信息:token 影响语法分析、属性影响翻译(这个 token 里词素之间的区别)

注意:关键字(有一定意义,如 if, else) keyword!= 保留字
token 的属性
e.g. E:=M*C**2
<id, 符号表中E对应项指针>
<assign_op,>
<id, 符号表中M对应项指针>
<mult_op,>
<id, 符号表中C对应项指针>
<exp_op,>
<num, 整型值2>
词法错误较少发生,但一旦发生就无法被词法分析器发现,因为存在 ambiguity
发生的情况:剩余输入的前缀和任何一个模式都匹配不上
错误修复:删除、插入、替换、交换字符
缓冲技术,缓解磁盘访问对性能的影响
磁盘 -> 缓冲区 -> 词法分析器
双缓冲:缓冲区 1 词法分析,缓冲区 2 读取磁盘
哨兵(sentinel)技术:在缓冲区末端添加标记,避免边界判定
正则表达式与转换图
相关术语:
- 字母表 alphabet:符号的有穷集合
- 符号串 string/句子 sentence:字母表中符号组成的有穷序列
- 前缀 prefix、后缀 suffix
- 子串 substring、子序列 subsequence
- 语言 Language:给定字母表的任意符号串集合
符号串的运算:
- 连接 concatenation(看作积 product)
- 幂 exponentiation
语言的运算:并 union、连接、闭包 closure、正则 positive 闭包
语言运算 <-> 正则表达式运算
正则表达式 regular expression
利用符号表中符号,遵循一组规则构成特定的符号串集合(描述 pattern)
正则表达式 r 表示正规集 regular set/语言 L (r)
正则表达式等价 equivalent:r = s 则 L (r)=L (s)
正则表达式的运算规律:
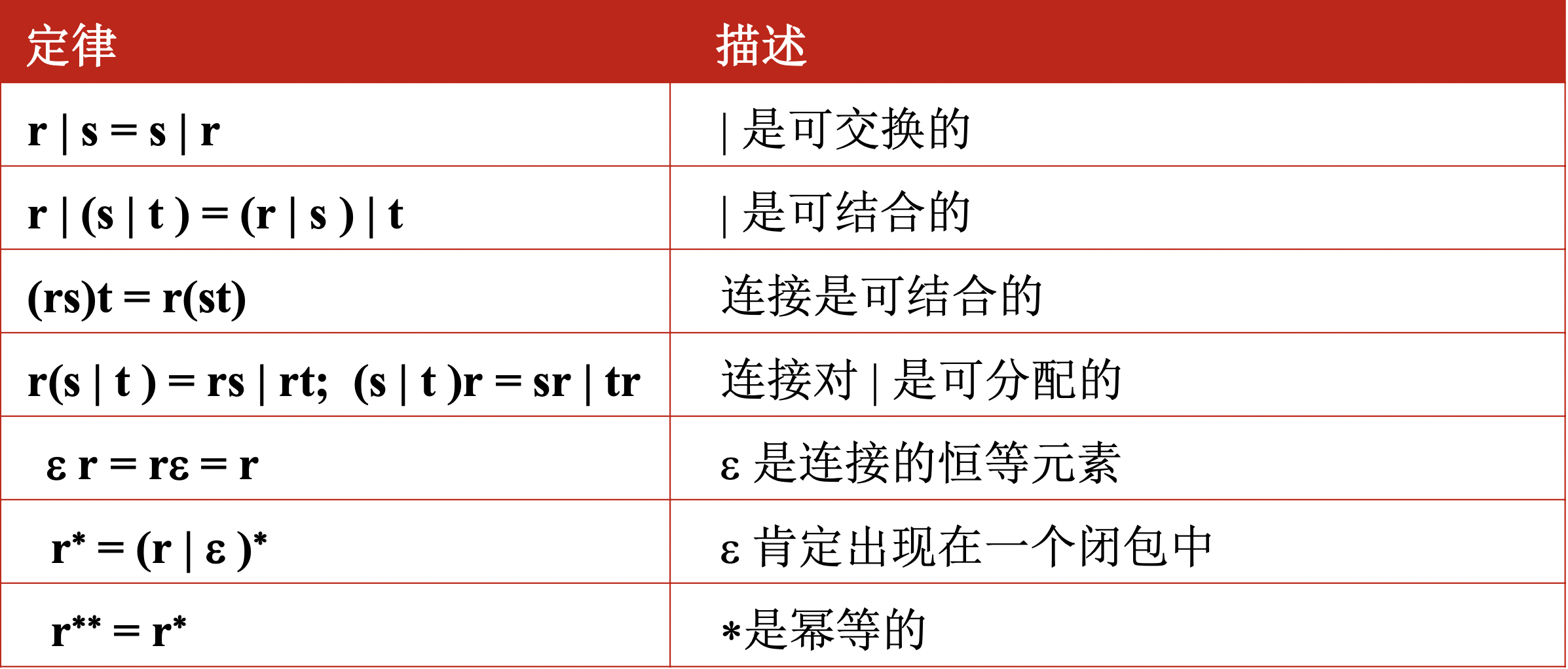
正规定义 regular definition:给正则表达式命名
符号简写:
+:一个或多个?:0 个或 1 个- 字符集:
[abc]-> a|b|c; [a-z]=a|b|...|z
更多正则表达式的基本语法见 正则表达式 30 分钟入门教程
正则表达式只能表示:有限的重复/一个给定结构的无限重复
无法描述平衡/嵌套的结构,如 {wcw|w是a、b组成的符号串}
转换图
转换图 transition diagram:
- 顶点:词法分析的某个状态
- 已读入符号串
- 带字符的边:指出输入某个字符时的状态转换
- 下一符号、应采取的动作
- 词法分析:从 start 初态开始读入字符、转换状态,到双圈终态 accept
- 星号表示将输入退回一个单词
词法分析从左到右读字符串,每次识别一个 token 实例;
已读入符号串前缀 + 未读入符号串,与模式匹配;
可能需要 lookahead 判断当前是否是一个 token 的结尾、下个 token 的开始;
最长匹配规则(匹配某个 pattern 的最长前缀),lookahead,不符合则回退;
可能需要结合上下文来识别是否是关键字。
e.g.标识符和关键字的转换图
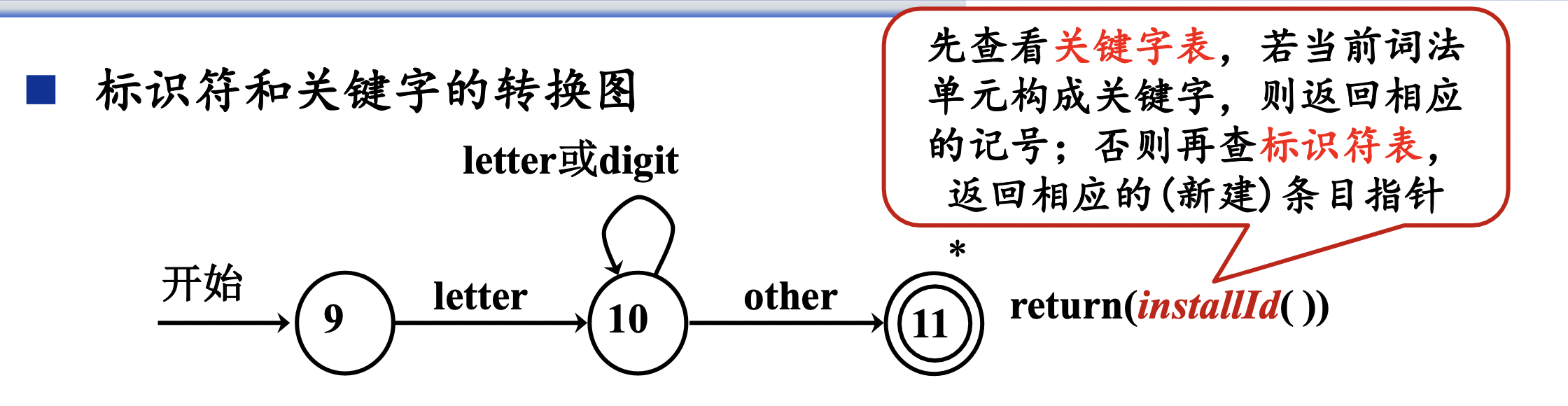
状态转换图的实现:
- 为每个状态构造一段代码
- 普通状态:读取字符、每条出射边根据字符转换状态
- 终态:返回 token 和值
- 错误处理
- 尝试其他状态转换图,若与任何 token 都不匹配,词法错误
具体到代码上,使用 switch-case 进行状态的区分,每个 case 表示一种状态,在每个状态读入一个 char,根据 char 是什么决定下一个状态;
如果无法匹配状态,就进入 fail() 函数,尝试其他的状态图,也就是再使用 switch-case 切换 start 的值。
int state = 0, start = 0;
int lexical_value; /* “返回” 词法值 */
int fail()
{ forward = lexeme beginning;
switch (start) {
case 0: start = 9; break;
case 9: start = 12; break;
case 12: start = 20; break;
case 20: start = 25; break;
case 25: recover(); break;
default: /* compiler error */
}
return start;
}
Lex 程序
lex 程序 (. l) 的结构和上一章中提到的 Yacc 程序类似,也分成定义段、规则段和用户子程序段三个部分。
/*P1: 定义段*/
%{
// include头文件、函数、类型等声明,这些声明会原样拷到生成的.c文件中。
#include %3Cmain.h%3E
extern "C"//为了能够在C++程序里面调用C函数,必须把每一个需要使用的C函数,其声明都包括在extern "C"{}块里面,这样C++链接时才能成功链接它们。extern "C"用来在C++环境下设置C链接类型。
{ //yacc.y中也有类似的这段extern "C",可以把它们合并成一段,放到共同的头文件main.h中
int yywrap(void);
int yylex(void);//lex生成的词法分析函数,yacc的yyparse()里会调用它,如果这里不声明,生成的yacc.tab.c在编译时会找不到该函数
}
int num_lines = 0, num_chars = 0; //统计行数和字符数
%}
//正规定义
/*非数字由大小写字母、下划线组成*/
nondigit ([_A-Za-z])
/*一位数字,可以是0到9*/
digit ([0-9])
/*整数由1至多位数字组成*/
integer ({digit}+)
/*标识符,以非数字开头,后跟0至多个数字或非数字*/
identifier ({nondigit}({nondigit}|{digit})*)
/*一个或一段连续的空白符*/
blank_chars ([ \f\r\t\v]+)
%%
/*P2: 规则段 */
p1 {action1}
p2 {action2}
...
pn {actionn}
//p:正则表达式;action:动作,当字符流前缀和p匹配时(识别出对应单词的词素)该做什么动作
/*
这个阶段的一些定义:
yylval 定义在 lex.yy.c中,它保存所返回token的属性值
yytext 指向当前识别出的词素的开始字符
yyleng 词素的长度
*/
//会从前往后逐个匹配,所以更一般的如.放在最后
{blank_chars} {} //遇空白符,忽略
\n {++num_lines; ++num_chars;} //遇回车,相应增加行数和字符数
. {++num_chars;} //匹配除回车外任意字符,增加字符数
%%
/*P3: 用户子程序段*/
main(int argc, char *argv[])
{
//参数保存在文件里,命令行输入
++argv, --argc; //跳过程序名
if(argc>0)
yyin = fopen(argv[0], "r"); //默认输入对象打开指定文件
else yyin = stdin; //如果没有指定文件,则将标准输入作为输入
yylex(); //识别
printf("# of lines = %d, # of chars = %d\n", num_lines, num_chars);
}
有限自动机
非确定有限自动机 NFA/确定有限自动机 DFA 的区别:前者允许 e 边、允许一个状态多条边相同符号;后者不允许,状态转换确定唯一的结果
正则表达式 -> 识别程序 recognizer
NFA
表示为五元组 M = {S, Σ, δ, s0, F},其中:
S:有限状态集Σ:输入符号集δ:状态转换函数,δ(s,a)=S'表示当前状态 s,输入符号 a,下一个状态在集合 S’中s0:唯一初态F:终态集(可空)
状态转换矩阵,横向表头是输入符号,纵向是状态,表格中是状态转换结果
NFA 接受符号串 x = 存在一条初态到终态的路径,路径上的符号组成 x
注意:同一个符号串可能存在多条路径,不是每条都表示接受
处理未定义状态转换:定义一个额外的 dead state,所有未定义状态转换都指向它,它指向自身
词法分析器可以用一组 NFA 描述,每个 NFA 表示一个单词
正则表达式到 NFA
算法描述:
- 对每个基本符号、e -> 简单 NFA
- 子正则表达式通过定义规则的操作(连接、或、闭包)构造复杂正则表达式
- 子 NFA 组合为复杂 NFA
构造规则:
1.
 2. s|t
2. s|t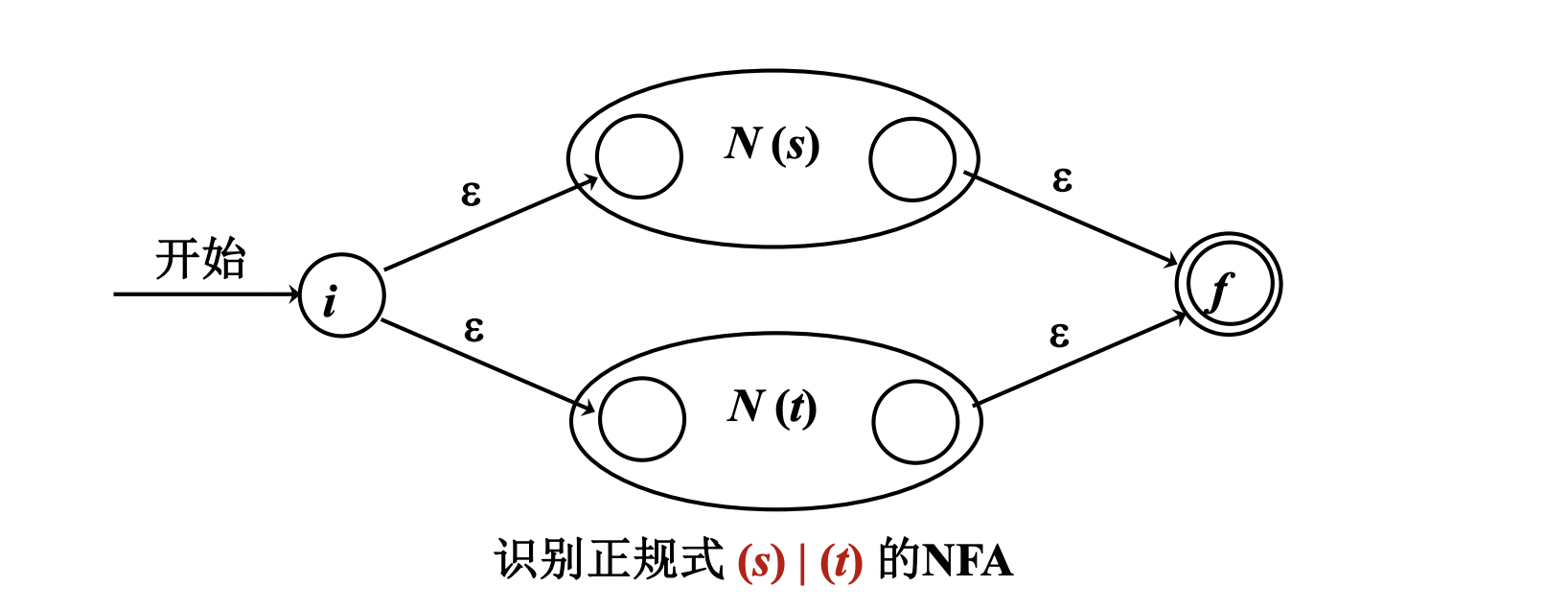 3. st
3. st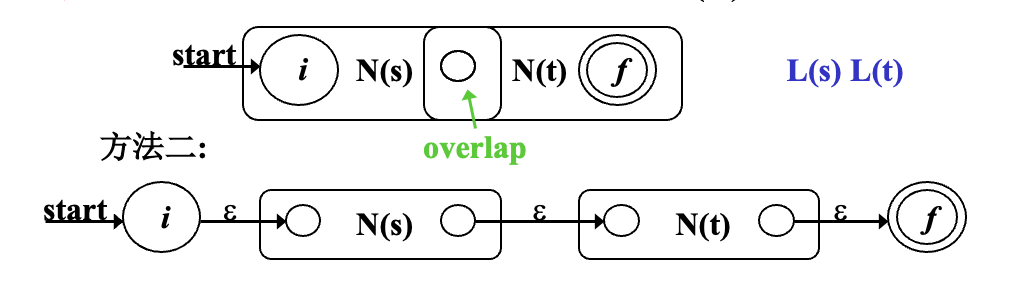 4. s*
4. s*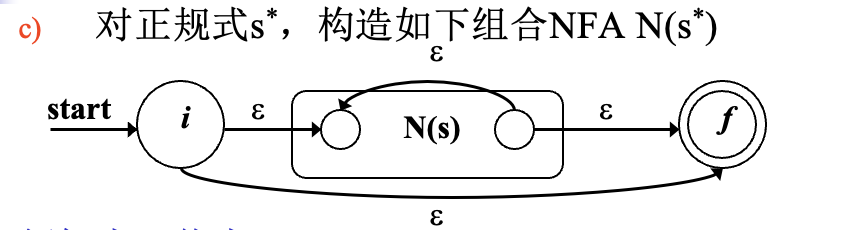
注意:
- 状态数最多是正则表达式中符号和算符总数的两倍
- 有且只有一个初态、一个终态
- 每个状态或者有一条标记为某个 a 的输出边,或者至多有两条 e 输出边
- 状态取名要小心
构建 NFA 首先要将其分解成树状,然后从底向上依次组合
NFA 到 DFA
任何符号串 N 和 D 结果一致 -> D 的一个状态对应 N 的一个状态子集
操作:
e-closure(s)e 闭包:s 以及从 s 出发仅通过(数量不限条) e 边可到达的所有状态的集合e-closure(T):\(\bigcup\epsilon-closure (s), s\in T\)δ(T,a):\(\bigcup\delta (s, a), s\in T\)
递推算法:
- N 的初态的闭包
T = e-closure(s0)即为 D 的初态 A - 对每个可能的路径 a,从 T 对 a 进行状态迁移
e-closure(δ(T, a)),即从 A 对 a 状态迁移,这个集合或对应一个 DFA 里已有的状态,或对应一个新状态 - 重复,直至不产生新的状态集合
注意:
- 状态集合(DFA 状态)可以重合
- 子集构造法不一定得到最简的 DFA
基于 NFA 实现词法分析器
为 Lex 程序中每个正则表达式构造 NFA
寻找与模式匹配的输入串的“最长前缀”
- 计算下一状态集,有终态加入就记录当前输入指针和匹配的模式;如果多个终态,取 Lex 程序中位置最靠前的模式
- 读入字符直至终止 terminal 状态(当前状态集对输入符号无状态转换)
- 输入指针退回对应位置可得 lexeme
DFA 化简
化简转换函数是全函数的 DFA
部分函数 -> 全函数:加入 dead state 将缺失状态都指向它
可区分(distinguishable)的状态:
将状态分成不相交的子集(初始时按是否为接受状态划分),存在一个输入符号,使得两个状态转换后指向不同子集
反之,不可区别就是没有一个输入符号能将二者划开
从终态“逆向”计算,寻找所有可被区分的状态组:
- 初始,两个组:终态、非终态
- 考察子集 A 的转换状态,若转换后属于不同状态组,则将 A 对应划分
- 检查完所有输入符号仍不能区分,则合并
- 继续分解
e.g.
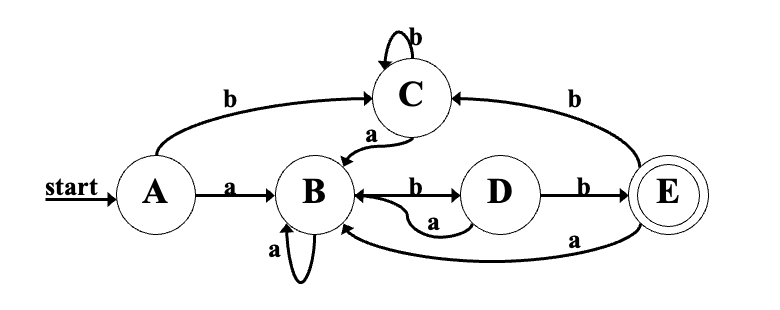
1. {E},{A,B,C,D} //按状态是否接受划分子集
2. 考察每个子集的状态转换
move({A,B,C,D},a) = {B}
move({A,B,C,D},b) = {C,D,E} //转换后状态落入不同子集
说明 {A,B,C,D} 可区别
3. 继续分解,当前划分为 {E},{D},{A,B,C}
4. ...